Skip to content

rawoctopus/CrackingTheCodingInterview

BranchesTags

Folders and files

NameName
Last commit message
Last commit date

Latest commit

 

History

3 Commits
README.md
README.md
 
 

Repository files navigation

스택과 큐

스택(Stack)

  • 데이터를 쌓아 올린다(stack)는 의미 = LIFO(Last In First Out)

  • 스택에 존재하는 연산

    • pop() : 스택에서 가장 위에 있는 항목을 제거한다.
    • push(item) : item 하나를 스택의 가장 윗 부분에 추가한다.
    • peek() : 스택의 가장 위에 있는 항목을 반환한다.
    • isEmpty() : 스택이 비어 있을 때에 true를 반환한다.

  • 데이터 추가(push) 혹은 삭제(pop)연산은 상수 시간에 가능하지만 이외에 다른 연산은 상수 시간으로 불가능.

  • 재귀(recursive) 알고리즘을 사용할 때 스택이 유용하다.

    • 재귀적으로 함수를 호출해야 하는 경우에 임시 데이터를 스택에 넣어 주고, 재귀 함수를 빠져 나와 퇴각 검색(backtrack)을 할 때는 스택에 넣어 두었던 임시 데이터를 빼 줘야 한다. 이런 과정들을 직관적으로 가능하게 해준다.
    • 재귀 알고리즘을 반복적 형태(iterative)를 통해서 구현할 수 있게 해준다.

  • 구현

    C

    #include <stdio.h>

#define MAX_SIZE 100
#define TRUE 1
#define FALSE 0

int stack[MAX_SIZE];
int top = -1;

int isEmpty() {
    if(top < 0)
        return TRUE;
    else
        return FALSE;
}

int isFull() {
    if(top > MAX_SIZE)
        return TRUE;
    else
        return FALSE;
}

void push(int value) {
    if(isFull() == TRUE)
        printf("Stack is full!");
    else
        stack[++top] = value;
}

int pop() {
    if(isEmpty() == TRUE) {
        printf("Stack is empty!");
        return -1;
    }
    
    else
        return stack[top--];
}

int peek() {
    if(isEmpty() == TRUE) {
        printf("Stack is empty!");
        return -1;
    }
    
    else
        return stack[top];
}

큐(Queue)

  • 매표소 앞에 서 있는 사람들이 움직이는 형태 = FIFO(First In First Out)

  • 큐에 존재하는 연산

    • add(item) : item을 리스트의 끝부분에 추가한다.
    • remove() : 리스트의 첫 번째 항목을 제거한다.
    • peek() : 큐에서 가장 위에 있는 항목을 반환한다.
    • isEmpty() : 큐가 비어 있을 때에 true를 반환한다.

  • 너비 우선 탐색(Breadth First Search)을 하거나 캐시를 구현하는 경우에 종종 사용 된다.

    • 처리해야 할 노드의 리스트를 저장하는 용도로 큐 사용.

  • 구현

    C

    #include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define TRUE 1
#define FALSE 0

typedef struct Node {
    int data;
    struct Node *next;
}Node;

typedef struct Queue {
    Node *front; //맨 앞(꺼낼 위치)
    Node *rear; //맨 뒤(보관할 위치)
    int size; //보관 개수
}Queue;

void initQueue(Queue *queue) {
    queue->front = queue->rear = NULL; //front, rear NULL로 설정
    queue->size = 0; //보관 개수 0으로 설정
}

int isEmpty(Queue *queue) {
    if(queue->size == 0)
        return TRUE;
    return FALSE;
}
//add 연산
void enqueue(Queue *queue, int data) {
    Node *newNode = (Node*)malloc(sizeof(Node)); //새 노드 생성
    newNode->data = data; //새 노드에 enqueue 할 값 넣어줌
    newNode->next = NULL;
    
    if(isEmpty(queue) == TRUE) //큐가 비어있으면(큐에 아무것도 없으면 처음 넣은 값이 맨 앞)
        queue->front = newNode;
    else //큐에 값이 있을 때
        queue->rear->next = newNode; //원래 맨 마지막에 있던 노드의 다음 노드가 새로운 노드
    
    queue->rear = newNode;
    queue->size++;
}
//remove 연산
int dequeue(Queue *queue) {
    if(isEmpty(queue) == TRUE) //큐가 비어있으면
        return -1; //비어있다는 뜻으로 -1 리턴
    
    Node* front = queue->front;
    int data = front->data;
    queue->front = front->next;
    free(front);
    queue->size--;
    return data;
}

//peek 연산
int peek(Queue *queue) {
    return queue->rear->data;
}

면접문제

  1. 배열 한 개로 스택 세 개를 어떻게 구현할지 설명하라.

    답 : 고정 크기를 할당해주면 된다. 즉, 하나의 배열을 같은 크기의 세 부분으로 나누어 각각의 스택이 그 크기 내에서만 사용되도록 하면 된다.

    예시)

    • n 사이즈를 가진 arr[n]을 선언

    • 스택#1은 arr의 0 ~ n/3 인덱스까지 사용

    • 스택#2은 arr의 (n/3+1) ~ (2n/3) 인덱스까지 사용

    • 스택#3은 arr의 (2n/3+1) ~ (n-1) 인덱스까지 사용

  2. 기본적인 push와 pop 기능이 구현된 스택에서 최솟값을 반환하는 min 함수를 추가하려고 한다. 어떻게 설계할 수 있겠는가? push, pop, min 연산은 모두 O(1) 시간에 동작해야 한다.

    답 : temp 변수를 선언하여 각 스택의 상태마다(스택의 연산이 이뤄질때마다) 최소값을 최신화 시켜주는 방법이 있다. 하지만 더 좋은 방법은 최소값들을 기록하는 스택을 하나 더 두면 된다. 기존 스택의 사이즈가 n이고 가장 처음에 삽입된 원소가 최소값일 경우, 두 번째 스택에 하나의 원소만 보관하기 때문에 효율적이다.

  3. 접시 무더기를 생각해보자. 접시를 너무 높이 쌓으면 무너져 내릴 것이다. 따라서 현실에서는 접시를 쌓다가 무더기가 어느 정도 높아지면 새로운 무더기를 만든다. 이것을 흉내 내는 자료구조 SetOfStacks를 구현해 보라. SetOfStacks는 여러 개의 스택으로 스택으로 구성되어 있으며, 이전 스택이 지정된 용량을 초과하는 경우 새로운 스택을 생성해야 한다. setOfStacks.push()와 SetOfStacks.pop()은 스택이 하나인 경우와 동이랗게 동작해야 한다. (다시 말해, pop()은 정확히 하나의 스택이 있을 때와 동일한 값을 반환해야 한다.)

    답 : 각각의 스택 객체를 담을 List 객체를 이용한다.

    class SetOfStacks {
    //여러개의 스택을 담을 Container(List)
    ArrayList stacks = new ArrayList();

    public void push(int v) {
        Stack last = getLastStack();
        //마지막 스택이 꽉 차지 않았으면 그 스택에 추가
        if(last != null && !last.isFull()) 
            last.push(v);
        //새로운 스택을 생성하여 스택 리스트에 추가
        else {
            Stack stack = new Stack(capacity);
            stack.push(v);
            stacks.add(stack);
        }
    }
    
    int pop() {
        Stack last = getLastStack();
        //list 자체에 스택 객체 자체가 없으면
        if (last == null) throw new EmptyStackException();
        int v = last.pop();
        //마지막 스택에서 pop 한뒤 그 마지막 스택의 사이즈가 0이되면(비어있으면) 스택 리스트에서 지움.
        if (last.size == 0) stacks.remove(stacks.size() - 1);
        return v;
    }
}

  4. 스택 두 개로 큐 하나를 구현한 MyQueue 클래스를 구현하라.

    답 : 큐와 스택의 주된 차이는 pop과 peek의 순서다.

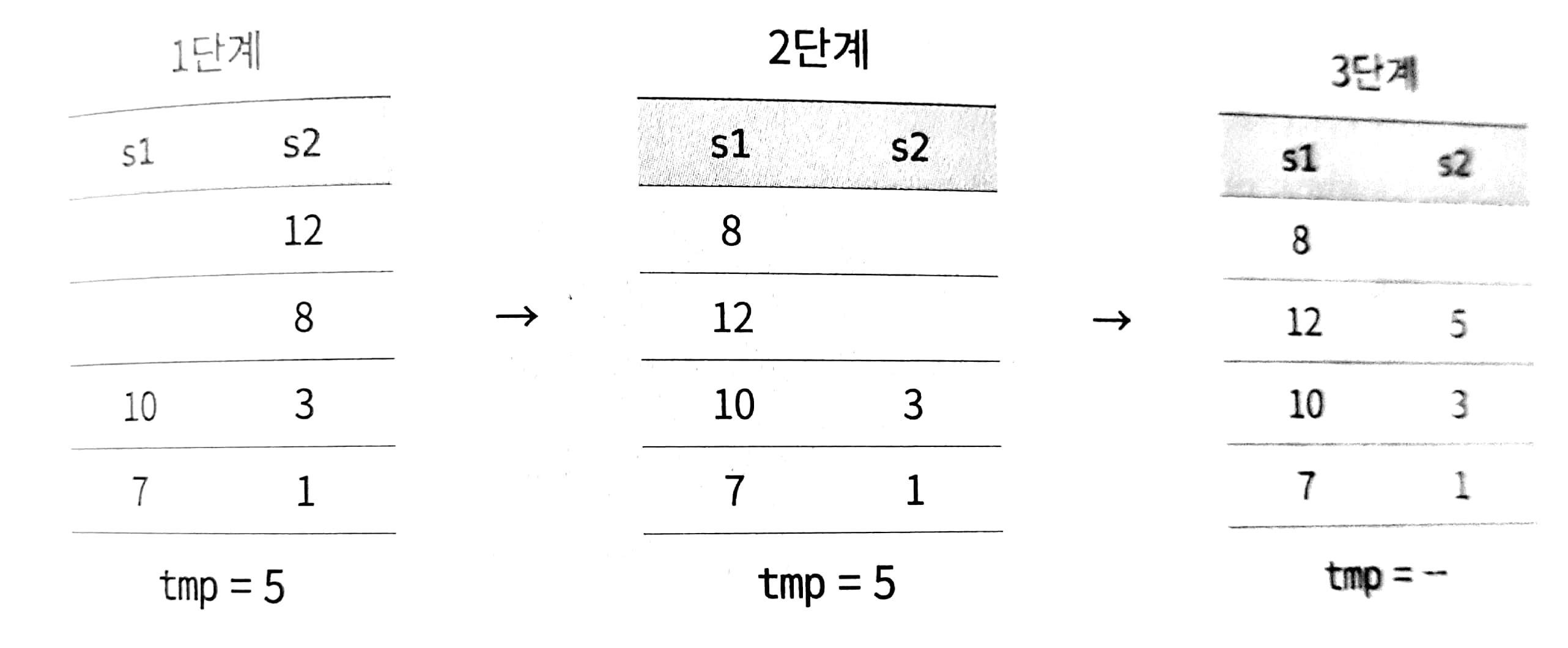
  5. 가장 작은 값이 위로 오도록 스택을 정렬하는 프로그램을 작성하라. 추가적으로 하나 정도의 스택은 사용해도 괜찮지만, 스택에 보관된 요소를 배열 등의 다른 자료구조로 복사할 수는 없다. 스택은 push, pop, peek, isEmpty의 네 가지 연산을 제공해야 한다.

    답 : 우선 s1에서 5를 꺼내서 임시 변수에 보관한 다음, s2의 12와 8을 s1로 이동시킨다. 그런 다음 5를 s2에 넣는다. 그리고 다시 s1에 있는 8과 12를 s2에 넣어준다.

    KakaoTalk_Photo_2019-07-27-03-39-34

    void sort(Stack s) {
    Stack r = new Stack();
    while(!s.isEmpty()) {
        /* s의 원소를 정렬된 순서로 r에 삽입한다. */
        int tmp = s.pop();
        while(!r.isEmpty() && r.peek() > tmp) {
            s.push(r.pop());
        }
        r.push(tmp);
    }
    
    /* r에서 s로 원소를 다시 옮겨준다. */
    while(!r.isEmpty()) {
        s.push(r.pop());
    }
}

    시간 복잡도 : O(N^2)

    공간 복잡도 : O(N)

  6. 먼저 들어온 동물이 먼저 나가는 동물 보호소(animal shelter)가 있다고 하자. 이 보호소는 개와 고양이만 수용한다. 사람들은 보호소에서 가장 오래된 동물부터 입양할 수 있는데, 개와 고양이 중 어떤 동물을 데려갈지 선택할 수 있다. 하지만 특정한 동물을 지정해 데려갈 수는 없다. 이 시스템을 자료구조로 구현하라. 이 자료구조는 enqueue, dequeueAny, dequeueDog, dequeueCat의 연산을 제공해야 한다. 기본적으로 탑재되어 있는 LinkedList 자료구조를 사용해도 좋다.

    답 : 개와 고양이를 별도의 큐로 관리. 그리고 그 두 큐를 AnimalQueue라는 클래스로 감싸는 것. 그리고 각 동물이 동물 보호소에 들어온 시기를 알려줄 timestamp를 기록한다.

트리와 그래프

트리

  • 트리는 노드로 이루어진 자료구조다.
  • 트리는 하나의 루트 노드를 갖는다.
  • 루트 노드는 0개 이상의 자식 노드를 갖고있다.
  • 그 자식 노드 또한 0개 이상의 자식 노드를 갖고 있고, 이는 반복적으로 정의된다.
  • 트리에는 사이클이 존재할 수 없다.
  • 노드들은 특정 순서로 나열될 수도 있고 그렇지 않을 수도 있다.
  • 각 노드는 어떤 자료형으로도 표현이 가능하며, 각 노드는 부모 노드로의 연결이 있을수도 있고 없을 수도 있다.

트리 종류

  • 트리 vs 이진 트리

    • 이진 트리(binary tree)는 각 노드가 최대 두 개의 자식을 갖는 트리를 말한다.
    • 모든 트리가 이진 트리는 아니다.

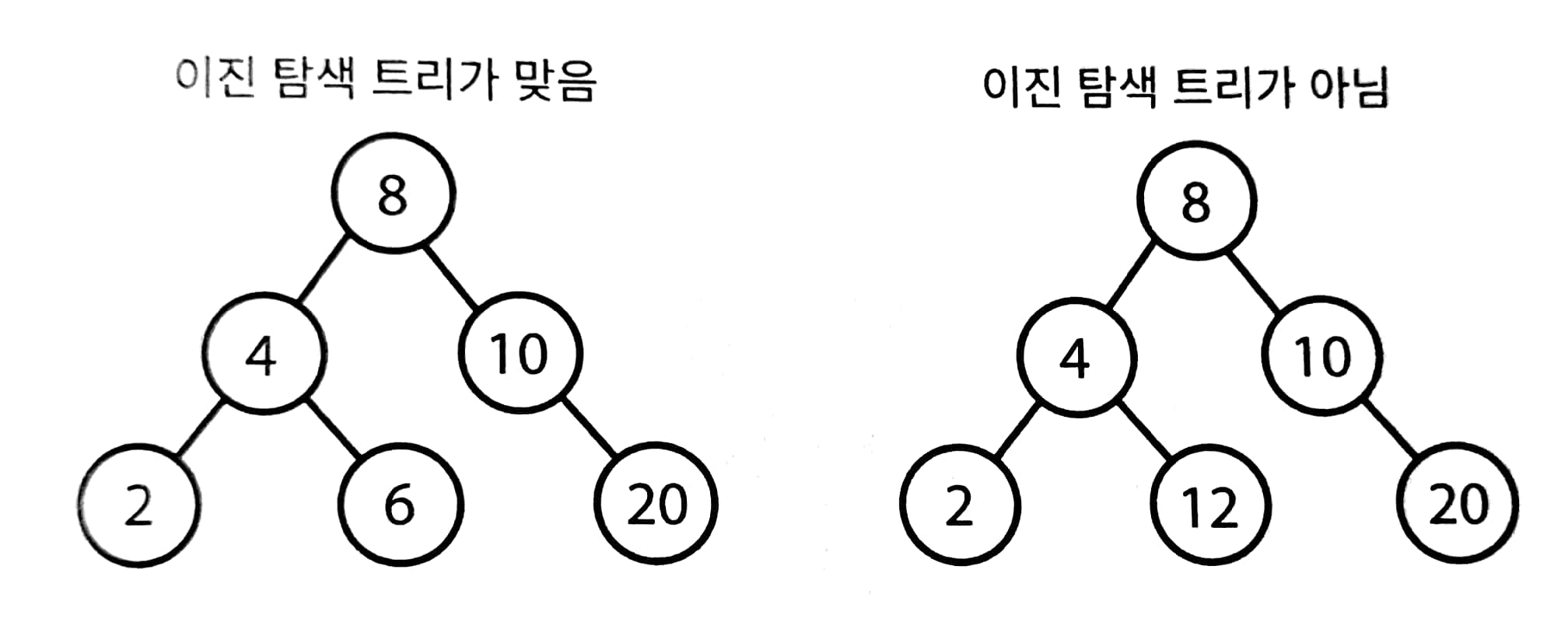
  • 이진 트리 vs 이진 탐색 트리

    • 이진 탐색 트리 : 모든 노드가 '모든 왼쪽 자식들 <= n < 모든 오른쪽 자식들' 속성이 있는 이진 트리를 말한다.
    • 면접 때 트리 문제가 주어지면 이진 탐색 트리일 것이라고 가정해버리는 경우가 많은데, 면접관에게 확실히 물어볼 것.
    • 좀 헷갈릴 수도 있을 만한 이진 탐색 트리 케이스 KakaoTalk_Photo_2019-07-27-04-10-26

  • 균형 vs 비균형

    • 왼쪽과 오른쪽 부분 트리의 크기가 완전히 같게 하는 것이 균형을 잡는다는 것을 의미하지는 않음.
    • 균형 트리의 일반적인 유형으로는 레드-블랙 트리와 AVL 트리 등이 있다.

  • 완전 이진 트리(Complete Binary Tree)

    • 트리의 모든 높이에서 노드가 꽉 차 있는 이진 트리.
    • 마지막 level은 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.

  • 전 이진 트리(Full Binary Tree)

    • 모든 노드의 자식이 없거나 정확히 두 개 있는 경우. 즉, 자식이 하나만 있는 노드가 존재해서는 안된다.

  • 포화 이진 트리(Perfect Binary Tree)

    • 전 이진 트리이면서 완전 이진 트리인 경우.
    • 모든 말단 노드(leaf)는 같은 높이에 있어야 하며, 마지막 단계에서 노드의 개수가 최대가 되어야 한다.
    • 노드의 개수가 정확히 2^(k-1) (k는 트리의 높이)개여야 한다. 하지만 면접에서 나온 이진 트리가 포화 이진 트리일 것이라고 생각x

이진 트리 순회

  • 중위 순회(In-order traversal)

    • 왼쪽 자식, 현재 노드, 오른쪽 자식 순서로 방문 및 출력
    • 이진 탐색 트리를 이 방식으로 방문하는 것이 오름차순으로 방문하는 것.

  • 전위 순회(Pre-order traversal)

    • 현재 노드, 왼쪽 자식, 오른쪽 자식 순서로 방문 및 출력

    • 가장 먼저 방문하게 되는 노드는 루트 노드

  • 후위 순회(Post-dorder traversal)

    • 왼쪽 자식, 오른쪽 자식, 현재 노드 순서로 방문 및 출력

    • 가장 마지막에 방문하게 되는 노드는 루트 노드

이진 힙(최소힙)

트리의 마지막 단계에서 오른쪽 부분을 뺀 나머지 부분이 가득 채워져 있다는 점에서 완전 이진 트리이며, 각 노드의 원소가 자식들의 원소보다 작다는 특성이 있다. 따라서 루트는 트리 전체에서 가장 작은 원소가 된다.

  • 삽입 연산(insert)
    • 새로운 원소는 밑바닥 가장 오른쪽 위치로 삽입 시작 (완전 트리 속성)
    • 새로 삽입된 원소가 제대로 된 자리를 찾을 때까지 부모 노드와 교환해 나간다.
    • O(logn) 소요 (n=노드의 개수)
  • 최소 원소 뽑아내기(extract_min)
    • 최소 원소는 언제나 가장 위에 놓이기 때문에 루트 노드 값을 가져오면 그만.
    • 루트 노드 값을 가져온 후에 다시 최소힙 상태를 만들어야 함
      • 루트 노드를 제거한 후에 힙에 있는 가장 마지막 원소(밑바닥 가장 왼쪽에 위치한 원소)와 교환한다.
      • 그 다음 힙의 성질 만족하도록 부모 노드와 교환해 나가며 제 자리를 찾게 한다.
    • O(logn) 소요

트라이(접두사 트리)

접두사 : 어떤 단어의 앞에 붙어 뜻을 첨가하여 하나의 다른 단어를 이루는 말을 이른다. 예: ‘맨주먹·덧버선·풋사과·군소리’ 등에서 ‘맨―’·‘덧―', '풋-', '군-' 따위

n-차 트리(n-ary tree)의 변종으로 각 노드에 문자를 저장하는 자료구조이다. 따라서 트리를 아래쪽으로 순회하면 단어 하나가 나온다. null node라고도 불리는 '*노드'는 종종 단어의 끝을 나타낸다. 예를 들어, MANY 이후에 '*노드'가 나오면 MANY라는 단어가 완성되었음을 알리는 것이다. MA라는 경로가 존재한다는 사실은 MA로 시작하는 단어가 있음을 알려준다.

'*노드'의 실제 구현은 특별한 종류의 자식 노드로 표현될 수도 있다. 예를 들어 TrieNode를 상속한 TerminatingTrieNode로 표현될 수도 있다. 아니면 '*노드'의 '부모 노드'안에 불린 플래그(boolean flag)를 새로 정의함으로써 단어의 끝을 표현할 수도 있다.

트라이에서 각 노드는 1개에서 ALPHABET_SIZE + 1개까지 자식을 갖고 있을 수 있다(만약 '*노드' 대신 boolean 플래그로 표현했다면 0개에서 ALPHABET_SIZE까지)

그래프

트리(tree)는 그래프(graph)의 한 종류이지만 모든 그래프가 트리는 아니다. 트리는 사이클(cycle)이 없는 하나의 연결 그래프(connected graph)이다. 그래프는 단순히 노드와 그 노드를 연결하는 간선(edge)을 하나로 모아 놓은 것과 같다.

  • 그래프에는 방향성이 있을 수도 있고 없을 수도 있다.
  • 그래프는 여러개의 고립된 부분 그래프로 구성될 수 있다. (모든 정점간에 경로가 존재하는 그래프를 연결 그래프)
  • 그래프에는 사이클이 존재할 수도 있고 존재하지 않을 수도 있다. (사이클이 없는 그래프는 '비순환 그래프')
  • 인접리스트(adjacency list) : 한 정점과 그 정점에 연결된 정점들을 리스트에 저장하는 방식
  • 인접 행렬(adjacency matrix)
    • boolean matrix로써 matrix[i][j]가 true라면 i정점에서 j정점의 간선이 존재한다는 뜻.
    • 무방향 그래프를 인접 행렬로 표현한다면 대칭 행렬이 된다.
    • BFS(너비 우선 탐색)도 인접 행렬에서 사용 가능.
    • 어떤 노드에 인접한 노드를 찾기 위해서는 모든 노드를 전부 순회해야 하기 때문에 효율이 떨어짐.
  • 그래프 탐색
    • 깊이 우선 탐색(Depth-First Search, DFS) : 루트 노드에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법.
      • a와 이웃한 노드 b를 방문했다면, b에 이웃한 다른 노드들을 먼저 방문하고 다시 돌아와 a에 이웃한 노드를 방문하는 순서.
      • 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다. 그렇지 않으면 무한루프 빠질 수 있음.
    • 너비 우선 탐색(Breadth-First Search, BFS) : 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법.
      • 재귀적으로 동작하지 않음 (가장 많이 오해하고 있는 부분), 큐(queue) 사용
      • a 노드에서 시작한다고 했을 때, a 노드의 이웃 노드를 모두 방문한 다음에 이웃의 이웃들을 방문한다.
    • 양방향 탐색(bidirectional search) : 출발지와 도착지 사이에 최단 경로를 찾을 때 사용됨.
      • 출발지와 도착지 두 노드에서 동시에 BFS을 수행한 뒤, 두 탐색 지점이 충돌하는 경우에 경로를 찾는 방식.
    • 최단 경로 혹은 임의의 경로를 찾고 싶을 때는 BFS가 일반적으로 더 낫다.

면접문제

  1. 방향 그래프가 주어졌을 때 두 노드 사이에 경로가 존재하는지 확인하는 알고리즘을 작성하라.

    답 : 두 노드 가운데 하나를 고른 뒤 탐색 도중 다른 노드가 발견되는지 검사하면 된다. 중복되는 일을 피하기 위해서 방문한 노드는 '이미 방문했음'으로 표시해 두어야 한다.

  2. 오름 차순으로 정렬된 배열이 있다. 이 배열 안에 들어있는 원소는 정수이며 중복된 값이 없다고 했을 때 높이가 최소가 되는 이진 탐색 트리를 만드는 알고리즘을 작성하라.

    답 : 왼쪽 하위 트리의 노드의 개수와 오른쪽 하위 트리의 노드 개수를 가능하면 같게 맞춰야 한다. 즉, 루트 노드가 배열의 중앙에 오도록 해야 한다. => 트리 원소 가운데 절반은 루트보다 작고 나머지 절반은 루트보다 커야 한다는 것을 의미.

    [로직] : 배열 가운데 원소를 트리에 삽입한다 -> 왼쪽 하위 트리에 왼쪽 절반 배열 원소들을 삽입 -> 오른쪽 하위 트리에 오른쪽 절반 배열 원소들을 삽입 -> 재귀 호출 실행

    TreeNode createMinimalBST(int array[]) {
    return createMinimalBST(array, 0, array.length - 1);
}

TreeNode createMinimalBST(int arr[], int sratr, int end) {
    if(end < start)
        return null;
    
    int mid = (start + end) / 2;
    TreeNode n = new TreeNode(arr[mid]);
    n.left = createMinimalBST(arr, start, mid - 1);
    n.right = createMinimalBST(arr, mid + 1, end);
    return n;
}

  3. 이진 트리가 주어졌을 때 같은 깊이에 있는 노드를 연결리스트로 연결해 주는 알고리즘을 설계하라. 즉, 트리의 깊이가 D라면 D개의 연결리스트를 만들어야 한다.

    답 : 전위 순회(pre order traversal) 알고리즘을 이용하여 푼다. 재귀 함수를 호출할 때 level+1을 인자로 넘긴다.

    ArrayList<LinkedList<TreeNode>> createLevelLinkedList(TreeNode root) {
    ArrayList<LinkedList<TreeNode>> result = new ArrayList<>();
    //루트 방문
    LinkedList current = new LinkedList();
    if (root != null)
        current.add(root);
    
    while(currrent.size() > 0) {
        result.add(current); //이전 깊이 추가
        LinkedList parents = current; // 다음 깊이로 진행
        current = new LinkedList();
        for(TreeNode parent : parents) {
            //자식 노드들 방문
            if(parent.left != null) current.add(parent.left);
            if(parent.right != null) current.add(parent.right);
        }
    }
    return result;
}

About

No description, website, or topics provided.

Resources

Readme
Activity
Custom properties

Stars

1 star

Watchers

4 watching

Forks

0 forks
Report repository

Releases

No releases published

Packages

No packages published

Contributors 2

  •  
  •